A PageRank az informatikában egy olyan algoritmus, amely hiperlinkekkel összekötött dokumentumokhoz számokat rendel azoknak a hiperlink-hálózatban betöltött szerepe alapján. (Ezt a számot szintén PageRanknek nevezik.) A PageRank a Google internetes keresőmotor legfontosabb eleme. Larry Page és Sergey Brin (a Google alapítói) fejlesztették ki 1998-ban a Stanfordi Egyetemen.
A Google arra a feltételezésre épít, hogy a weboldalak készítői általában azokra az oldalakra linkelnek a saját lapjukról, amiket jónak tartanak, vagyis minden hiperlink felfogható egy-egy szavazatként a céloldalra. Minél több szavazatot kap egy oldal, annál fontosabb, de azt is figyelembe kell venni, hogy a szavazatot leadó oldal mennyire fontos. (Ez egy rekurzív definíció: az a fontos oldal, amire fontos oldalak mutatnak.) A PageRank a fontosság számszerűsítése.
A PageRank szó a Google bejegyzett védjegye. Az eljárást az USA-ban szabadalom védi (6,285,999. számú U.S.-szabadalom).
Szavazás
A fenti alapötlet szerint kezdetben minden oldalnak egy egységnyi szavazata van, amit egyenlően szétoszt azok között az oldalak között, amikre hivatkozik, és a más oldalaktól kapott szavazatokat is ugyanígy továbbosztja. Egy oldal PageRankje megegyezik a kapott szavazatok számával (ami nem feltétlenül egész szám). Ahhoz, hogy ez az eljárás jóldefiniált legyen, be kell vezetni egy d csillapító tényezőt: az oldalak a szavazatukból csak d részt osztanak tovább, (1-d)-t pedig megtartanak. (A mástól kapott szavazatokat teljesen továbbosztják.) Így a PageRankre a következő képlet adódik:
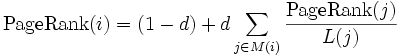
ahol M(i) azoknak az oldalaknak a halmaza, amik tartalmaznak linket az i. oldalra, L(j) pedig a j. oldalról kimenő linkek száma.
Normális esetben (ha kizártuk a lógó linkeket), ha a vizsgált hálózat N oldalból áll, akkor az egyes oldalak PageRankjeinek összege N lesz. Így a PageRank szavazás helyett úgy is elképzelhető, mint a kezdetben a weblapok között egyenletesen elosztott fontosság átcsoportosítása.
Sztochasztikus szörföző
A PageRanket úgy is felfoghatjuk, mint annak a valószínűségét, hogy odatalálunk az oldalra. A valószínűséget a sztochasztikus szörfözővel modellezzük, aki a weben bolyong, és minden lépésben véletlenszerűen, egyenletes eloszlás szerint kiválaszt egyet az oldalon található linkek közül, és azon halad tovább. (Más szóval véletlen bolyongást végez a hiperlinkek alkotta irányított gráfon.) Hogy ne essen csapdába valamelyik olyan részgráfban, amiből nem vezet kifelé link, a modellt kiegészítjük egy további elemmel: a szörföző minden lépésben 1-d valószínűséggel elunja magát, és egy (egyenletes eloszlás szerint) véletlenszerűen választott weblapra ugrik. Így, ha az n.-ik lépésben az egyes oldalakon tartózkodás esélyét a számok adják meg, akkor a következő lépés utáni valószínűségeket a  számok adják meg, akkor a következő lépés utáni valószínűségeket a
számok adják meg, akkor a következő lépés utáni valószínűségeket a
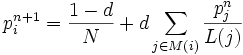
képlettel kapjuk.
Az egyes lépésekben felvett pozíciók mint valószínűségi változók sorozata egy irreducibilis és aperiodikus Markov láncot alkot, tehát létezik határeloszlása. (Ehhez szükséges a csillapító tényező: ha a gráf nem lenne erősen összefüggő márpedig egy véletlen gráf 1 valószínűséggel nem az , akkor a lánc reducibilis lenne.) Az oldal PageRankjét a határeloszlásban hozzá tartozó valószínűségként definiáljuk. Ez a következő rekurzív képletet adja a PageRankre:
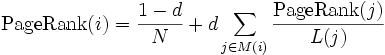
Ez nem azonos a szavazásos képlettel: az 1-d tényező itt le van osztva az összes oldal számával, tehát az így definiált PageRank az előzőnek éppen N-edrésze. Brin és Page eredetileg a sztochasztikus szörföző modelljéből vezette le a PageRank képletét, de eltévesztették a képletet, és az N nélküli változatot publikálták. Bár a későbbi cikkekben kijavították, mégis a hibás változat terjedt el, mert a gyakorlatban könnyebben számítható: N-t nehéz meghatározni, mert a kereső a folyamatosan változó világhálónak egyszerre mindig csak egy kis részét látja.
A sztochasztikus szörföző modellel definiált PageRank tehát egy valószínűségi eloszlás lesz: egy oldal PageRankje annak a valószínűsége, hogy nagyon sok véletlenszerű kattintás (és ugrás) után éppen arra az oldalra érkezünk. (A PageRank reciproka az oldal várható visszatérési ideje, azaz annak a várható értéke, hogy az oldalról elindulva hány lépés múlva érünk vissza oda.)
Lógó linkek
A lógó link (dangling link) olyan hivatkozás, ami egy zsákutcára mutat: egy olyan dokumentumra, ami egyáltalán nem tartalmaz linket. (Ilyenek gyakran előfordulnak, egyrészt mert a Google a HTML-en kívül számos más fájlformátumot is ismer , és ezek a formátumok általában nem tartalmaznak linkeket; másrészt mert a web feldolgozását valós időben végzi, és a még le nem töltött vagy fel nem dolgozott oldalakat üresnek látja.) Ezek a linkek gondot okoznak a PageRank számításakor, mert ha a sehova nem vezető oldalaknak is adunk PageRanket, akkor a rendszerben levő összes szavazat kevesebb lesz az oldalak számánál. A '98-as cikk szerint a Google a PageRank-számítás idejére átmenetileg kitörli ezeket a linkeket; hogy ez pontosan hogy történik, az nem derül ki a szövegből.
forrás:Wikipédia
Kapcsolódó linkek:
- Magyar pagerank toplista: http://pagerank.g-easy.hu
- PagRank mítoszok

